Search Algorithms
Properties of Search Algorithms
Completeness
Completeness is whether or not the algorithm is guaranteed to find a goal (provided at least one goal exists).
Optimality
Optimality is whether or not the algorithm is guaranteed to find the shallowest goal (i.e. the goal with the lowest cost).
Time Complexity
Time Complexity refers to the degree of time consumed by the algorithm.
Space Complexity
Space Complexity refers to the degree of memory space consumed by the algorithm.
Search Tree Terminology
Node: a state in the search problem
Edge: an action or a transition between states in the search problem
Branching Factor,
Shallowest Goal Depth,
Maximum Depth,
Heuristics
Heuristics are solution strategies by trial and error used to produce acceptable (optimal or sub-optimal) solutions to complex problems in a reasonably practical time. Heuristics aim to efficiently generate good solutions, but does not guarantee optimality. Heuristics:
- have short running times
- are easy to implement
- are flexible
- are simple
A heuristic function
Admissible Heuristic
An admissible heuristic function is one that never overestimates the cost of reaching a goal:
where
Breadth-First Search
Breadth-First Search involves searching the tree by expanding nodes into a queue data structure.
Search Path:
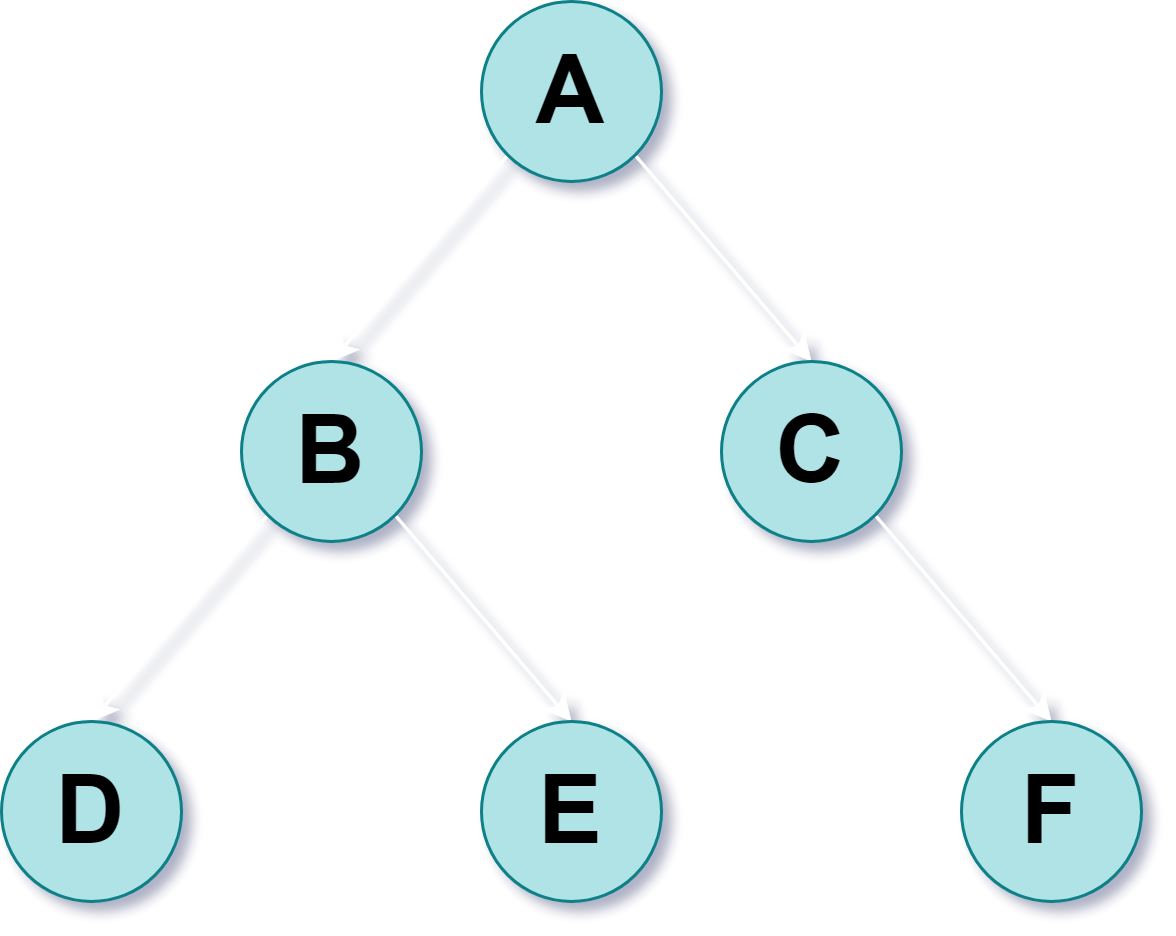
| Property | Remarks |
|---|---|
| Complete | Yes, if |
| Optimal | Yes, if path cost is equal to depth |
| Time Complexity | |
| Space Complexity |
Depth-First Search
Depth-First Search involves searching the tree by expanding nodes into a stack data structure.
Search Path:

| Property | Remarks |
|---|---|
| Complete | Yes, if |
| Optimal | No |
| Time Complexity | |
| Space Complexity |
Uniform-Cost Search
Uniform Cost Search involves searching the tree by expanding nodes into a priority queue data structure based on the cost of the path to each node.
Search Path:
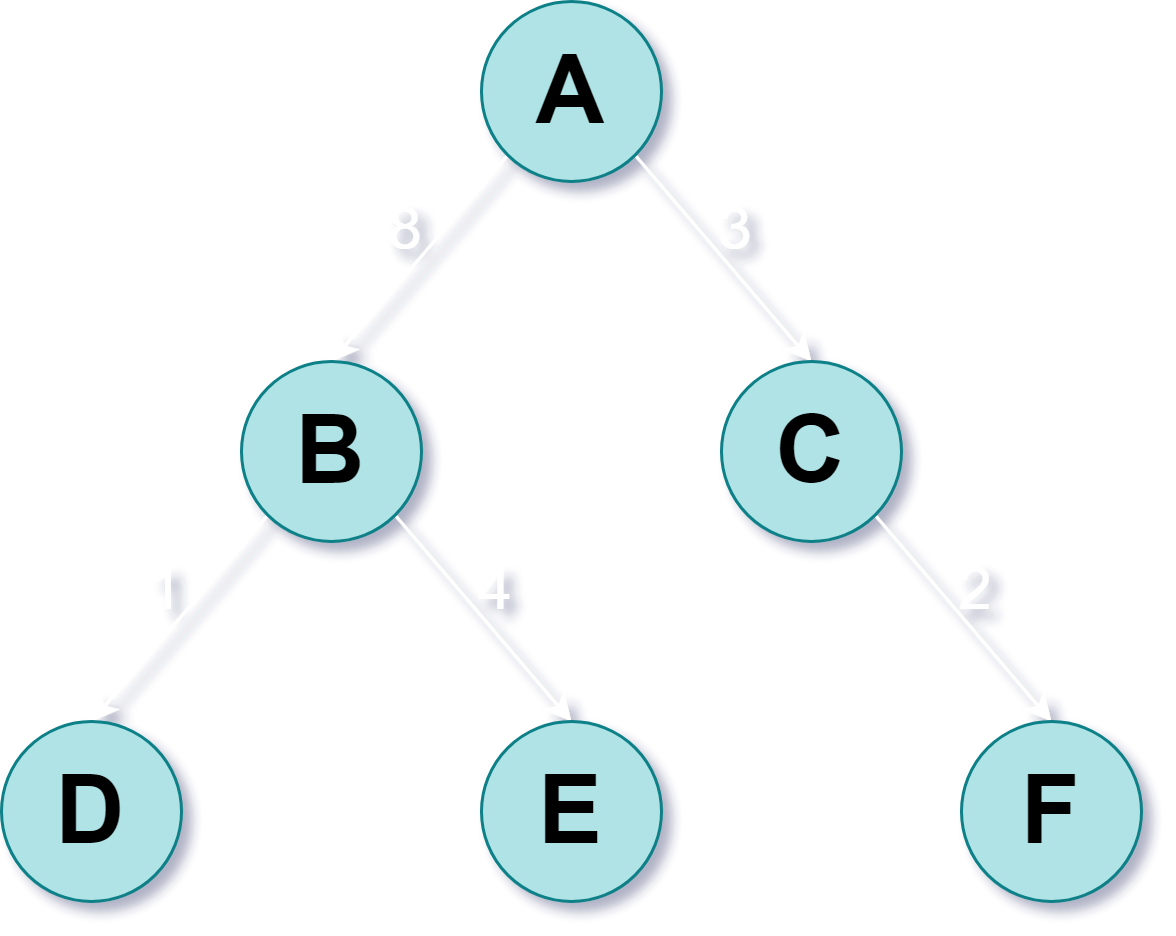
| Property | Remarks |
|---|---|
| Complete | Yes |
| Optimal | Yes |
| Time Complexity | |
| Space Complexity |
Depth-Limited Search
Depth-Limited Search involves searching the tree using Depth-First Search, but limiting the maximum expanded depth to an upper bound
Search Path

| Property | Remarks |
|---|---|
| Complete | Yes, if |
| Optimal | No |
| Time Complexity | |
| Space Complexity |
Iterative-Deepening Search
Iterative-Deepening Search involves searching the tree using Depth-Limited Search using incremental values of
Search Path
Search Path
Search Path

| Property | Remarks |
|---|---|
| Complete | Yes, if |
| Optimal | Yes, if path cost is equal to depth |
| Time Complexity | |
| Space Complexity |
Greedy Search
Greedy Search involves running Best-First Search with an evaluation function
| Property | Remarks |
|---|---|
| Complete | No |
| Optimal | No |
| Time Complexity | |
| Space Complexity |
Beam Search
Beam Search involves storing and expanding the
| Property | Remarks |
|---|---|
| Complete | No |
| Optimal | No |
| Time Complexity | |
| Space Complexity |
A* Search
A* Search involves running Best-First Search with an evaluation function
| Property | Remarks |
|---|---|
| Complete | Yes, if |
| Optimal | Yes, if |
Hill-Climbing Search
Hill-Climbing involves always traversing the node that decreases
| Property | Remarks |
|---|---|
| Complete | No |
| Optimal | No |
Max-Min Strategy
Max-Min Strategy (or the minimax algorithm) is a recursive backtracking algorithm that chooses the maximum or minimum value of the child nodes at any node.
| Property | Remarks |
|---|---|
| Complete | Yes, if tree is finite |
| Optimal | Yes, if opponent is optimal opponent |
| Time Complexity | |
| Space Complexity |