Reference Tracking

Consider a unity feedback system with reference signal $r(t)$$r(t)$, output signal $y(t)$$y(t)$, plant $P(s)$$P(s)$ and controller $C(s)$$C(s)$.

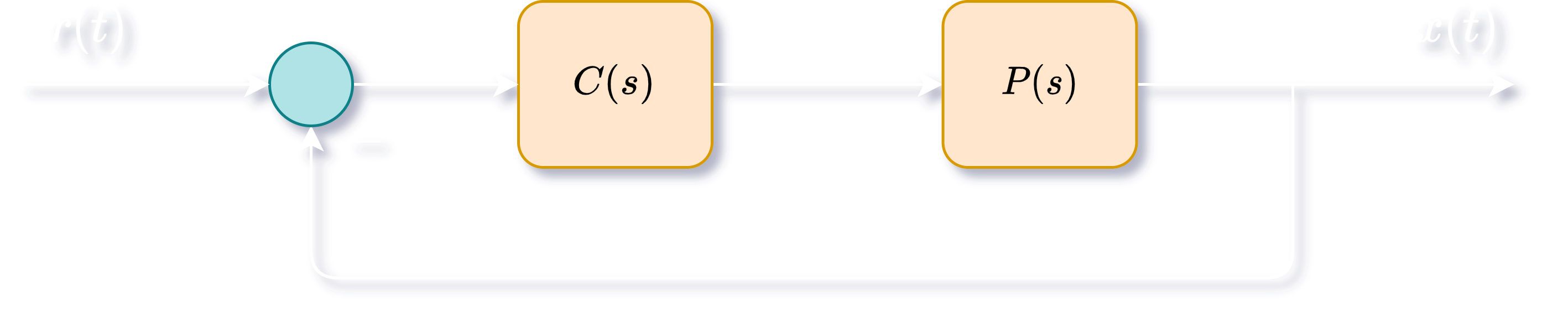
The transfer function from $r$$r$ to $y$$y$ is:

We can write $P(s)C(s)$$P(s)C(s)$ as:

where $s=0$$s = 0$ is not a root of $b(s)$$b(s)$.

For a reference signal of the form,

where k is a constant and m is a non-negative integer, we can assess the error function $e(t)=r(t)-y(t)$$e(t) = r(t) - y(t)$:

We know,

There value of $e_{ss}(t)$$e_{ss}(t)$ affects the tracking of the reference signal and depends on the relative values of $q$$q$ and $m$$m$.